|
|||||||||||||||||||
|
Class Abstraction Tool |
|
Johannes Kepler University Altenbergerstr. 69, 4040 Linz, Austria
|
|
|
||
|
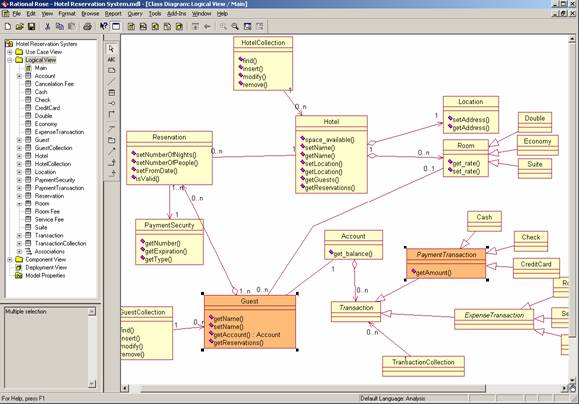
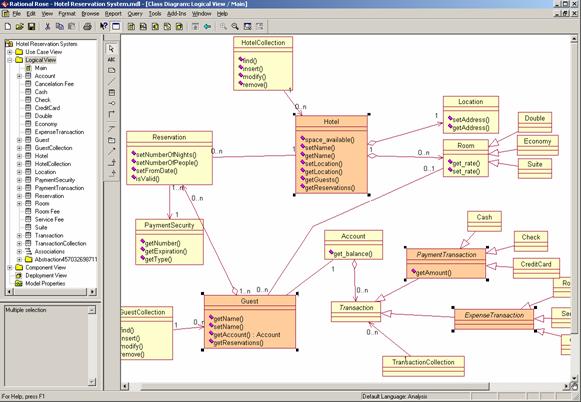
DOWNLOAD Click here to learn more about the technology that makes class abstraction possible. OVERVIEWWhen dealing with large class diagrams, designers can get overwhelmed easily with details. This document presents an approach for automated abstraction that allows designers to “zoom out” of class diagrams to investigate and reason about their bigger picture. The approach is based on a large number of abstraction rules that individually are not very powerful but when used together they can abstract complex class structures quickly. This paper presents those abstraction rules and an algorithm for applying them. Our technique was validated on over a dozen models where it was shown to be well-suited for model understanding, consistency checking and reverse engineering. This document presents the class abstraction tool in from of a mini tutorial. MINI TUTORIALThe class abstraction tool is fully integrated with IBM Rational Rose and very easy to use. In the following, we will present a mini tutorial on its use. Figure 1 depicts a simplified Hotel Management System (HMS) in IBM Rational Rose taken from [4]. The HMS consists of a set of classes and relationships. Both classes and relationships are further annotated with properties such as directionality or methods. We highlighted two classes in the figure as they will be discussed in the following abstraction scenario. We developed a transitive reasoning technique in collaboration with Rational Software. The technique can take arbitrary complex class patterns to infer transitive relationships between its classes. We define a transitive relationship to be the semantic equivalent of a collection of normal relationships. For instance, if two normal calling relationships exist (e.g., UML associations) so that A calls B and B calls C then, transitively, we can infer that A calls C. Transitive relationships are thus indirect relationships between classes.
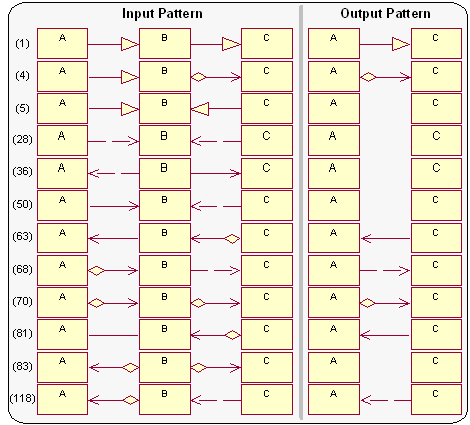
Figure 1. IBM Rational Rose depicting a simplified Hotel Reservation System A transitive relationship is always the result of a collection of direct relationships. By composing the properties of a collection of direct relationships one can infer properties of the transitive relationship. Properties of relationships include direction of call, type of relationship, or cardinality of association ends. If, say, two relationships have the same type and the same calling direction then transitively the two relationships can be composed into a single one of the same type and direction (see Rule 70 in Figure 2). Transitive relationships are thus a form of abstraction where the transitive relationship is semantically equivalent or weaker (less constrained) than the direct relationships it composes. Figure 2 gives an excerpt of about 121 transitive relationships defined in [4]. For instance, rule 1 states that if A inherits from B and B inherits from C (input pattern) then, transitively, A inherits from C (output pattern). Or Rule 118 states that if C depends on B, A is a part of B (diamond head), and A is called by B (arrowhead) then, transitively, C depends on A.
Figure 2. Subset of Transitive Abstraction Rules taken from [4] The given transitive abstraction rules are simple in nature. Most rules describe a collection of two input relationships that can be composed into a single output relationship. What makes this abstraction technique powerful is the large number of simple rules (121 rules for three types of class relationships and various properties). Given the simplicity of the rules, the abstraction algorithm is very fast (see empirical studies in [4]); however, at the expense of precision. UML relationship semantics are not well-treated in the current UML specification which may lead to uncertainties during transitive reasoning (e.g., A calling B and B calling C may not imply A calling C always). As input, the algorithm takes an arbitrary complex class structure and a list of ‘important classes’ (the cluster). The list of important classes is needed to distinguish between classes that may be abstracted and classes that may not. In Figure 2 the classes A and C are important and the class B is not important as it gets replaced (together with its relationships) by a higher-level relationship. A human has to make the decision on what classes are important as it depends on the circumstances and usage of the higher-level output.
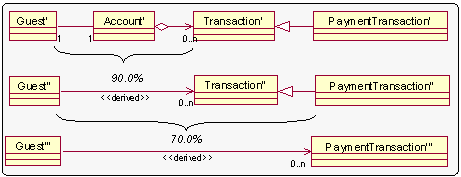
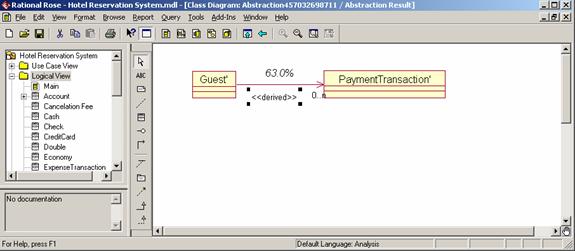
Figure 3. Transitive Relationship between two Classes Figure 3 shows the use of transitive (relational) reasoning in understanding the relationship between the user-defined, important, low-level classes Guest and Payment Transaction (from Figure 1). Although the two classes are not directly related to one another, a transitive relationship can be derived by eliminating the helper classes Account and Transaction. Figure 3 shows that the application of a rule eliminates the class Account first and the subsequent application of another rule (see [4] for all rules) eliminates the class Transaction. This results in a high-level relationship between the two important classes which is semantically equivalent to the replaced classes and all their relationships.
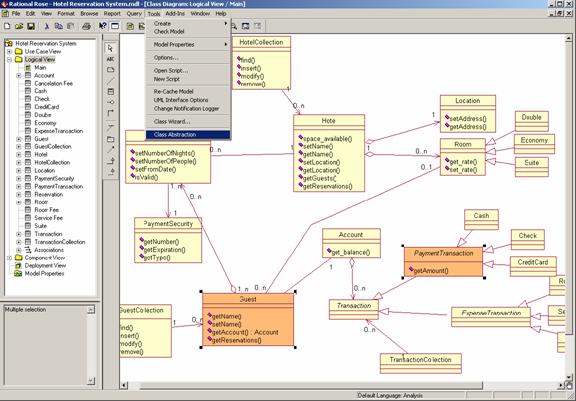
Figure 4. Invoking the Class Abstraction Tool on the two classes Guest and PaymentTransaction A user of our tool does not have to understand abstraction rules or how to apply them. The class abstraction tool simply requires a user to specify the important classes that should not be abstracted. For example, if we would like to understand the relationship between Guest and PaymentTransaction (as in the example above), the user only has to select the two classes (press and hold the control key while selecting multiple classes) and to invoke the abstraction tool through the tools menu (Tools:Class Abstraction). Figure 4 depicts this. As a result, the tool generates a new class diagram depicting only the previously selected, important classes and all relationships between them (direct and transitive ones).
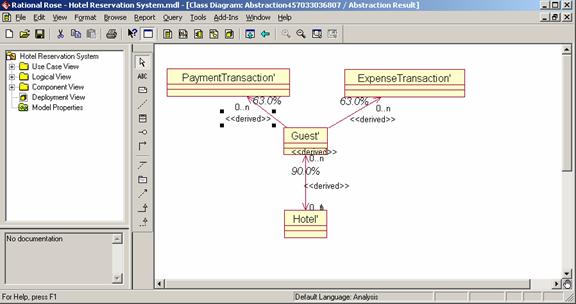
Figure 5. Abstracted Transitive Relationship between Guest and PaymentTransaction There is no restriction as to how many classes can be important. Figure 6 depicts the HMS class diagram again and four classes are selected as important classes (Guest, Hotel, PaymentTransaction, and ExpenseTransaction). Invoking the class abstraction tool results in the class diagram depicted in Figure 7 with the four important classes and all direct/transitive relationships between them It must be noted that it is generally of advantage of designate more classes as important classes for two reasons: 1. usability: designating more classes as important classes reduces the “degree of abstraction” and it is easier possible to evaluate the correctness of abstraction results 2. scalability: the tool explores all possible paths among the important classes. only those paths are abstracted that do not include any important classes. Since the searching for paths is expensive, it is better to have more important classes as they restrict the paths.
Figure 6. Abstracting the relationships between multiple classes
Figure 7. Abstraction result after abstracting multiple classes REFERENCES
|
||
|
|
||